Contents x
    Simulation Model basics
        Contents

        Simulation Model basics

            Article summary

            A Simulation Model is a collection of variables, which together represent something that could be observed, or controlled, in a virtual experiment.

            These variables can be numeric or categorical, so you could imagine a model of a plant with several variables:

            • Height (numeric) - the maximum height the plant achieves
            • Fertilized (categorical) - values "Yes" or "No" indicate whether the plant received a specific fertilizer
            • Weekday (categorical) - the day of the week the seed was planted

            Models can be much simpler than this. For example, a model of a coin could have:

            • Result (categorical) - values "Heads" and "Tails"

            When the simulation runs, the model will generate random data for each of the variables, depending on how they have been configured, for each sample.

            In the Model, all variables are equal
            In the Simulator, one variable is picked as the Response variable, while others can be used as Predictor variables. But in the Model there is no essential difference, any of the model's variables can be used in either role.

            Numeric variables

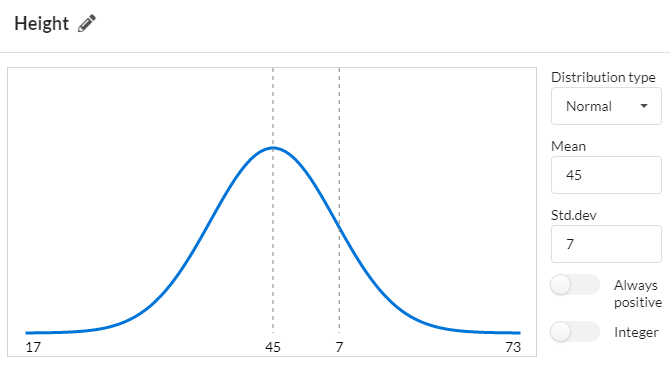
            The simplest numeric variable is one that varies randomly with a normal distribution, and it has values for the mean and the standard deviation:

            Categorical variables

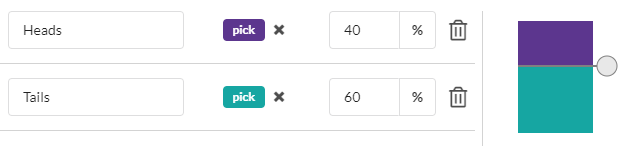
            Categorical variables have a list of possible values and each value has a probability of occurring. For example, this model of a coin that can be flipped - but isn't fair!

            Creating a Model

            You can create a model either by copying one from an existing simulation, copying an existing model, or creating one from scratch as described in this video:


            Editing a Model

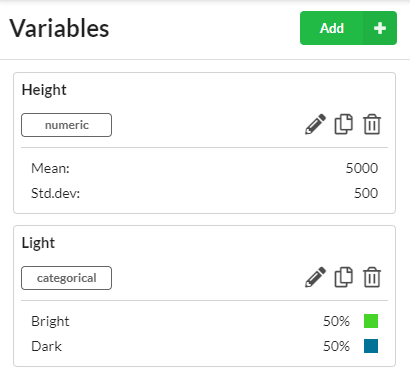
            The Simulation Model, when you open it with either the pencil icon on the model or the Edit simulation model left menu item, has a simple list of variables which you can use to add new variables, delete variables, and edit variable properties.

            Connecting variables

            By default, all variables are independent, and this can be used to model properties that are independent in real life. In the plant example at the top of this page you would expect the Weekday property to be completely independent of the final height of the plant. Right?

            The interesting stuff begins when you start connecting variables, to define a correlation or a causative relationship. Read more in the article Connecting variables in Simulation Models.


            Was this article helpful?
            What's Next